En el comienzo del tema 3 de Lenguaje Matemático se habla sobre relaciones lógicas; aunque no se explicite, la impresión que me dan es que son una especie de precursores o de forma primitiva de las funciones matemáticas, simplemente vistiendo ropaje de teoría de conjuntos. Se explica que las relaciones pueden ser de 4 tipos (en mis propias palabras, intentando no consultar el libro).
Primero tenemos que asumir que R es una relación incluyendo pares (x,y) con x e y provenientes de, digamos, un conjunto U (habitualmente, ese conjunto sería R, el de los números reales, y los pares resultantes de la relación provenientes del producto RxR).
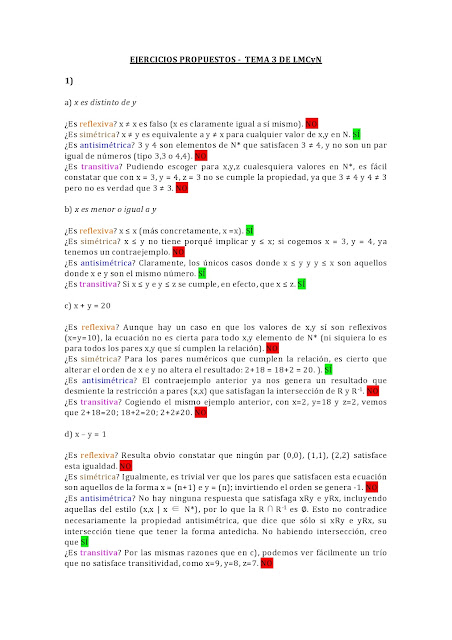
1) Reflexiva: una relación será reflexiva si para todo x perteneciente a U existe la relación xRx. Viéndolo bajo la forma de conjuntos, el conjunto R es reflexivo si contiene todos los pares (x,x) posibles a partir de los elementos de U. Un par de ejemplos, partiendo del conjunto U = {1,2,3,4}:
R = {(1,1), (1,3), (2,2), (2,1), (3,3)} NO ES REFLEXIVO: le faltaría incluír el par (4,4).
R = {1,1), (1,3), (2,2), (3,3), (3,4)} SÍ ES REFLEXIVO: tiene todos los pares (x,x) posibles.
2) Simétrica: una relación será simétrica si para todo par x, y perteneciente a U, si existe la relación xRy, entonces existe también la relación yRx. Técnicamente, se puede plantear como la afirmación de que si un conjunto R es simétrico, entonces contendrá a su inverso como subconjunto. De nuevo, partiendo del conjunto U = {1,2,3,4}:
R = {(1,2), (2,1), (3,1)} NO ES SIMÉTRICO: le faltaría incluír el par (1,3).
R = {(1,2), (2,1), (3,1), (1,3)} SÍ ES SIMÉTRICO. Para cada par xy del conjunto, existe un par yx. Nótese que no hace falta (como con la propiedad reflexiva) incluír todos los pares posibles del conjunto U; sólo para aquellos pares que están en R.
3) Antisimétrica: una relación será antisimétrica si para todo par x, y perteneciente a U, si hay algún caso en que xRy y yRx (no tiene porqué haberlos), necesariamente será porque x=y. No es posible que se de la situación con x e y diferentes. Técnicamente se plantea que la intersección de R y su recíproco serían un subconjunto del conjunto reflexivo (o sea, pares x,x). Partiendo del conjunto U = {1,2,3,4}:
R = {(1,2), (2,1), (3,1)} NO ES ANTISIMÉTRICO: ya que tenemos un caso por lo menos donde la intersección de R y su recíproco no es de la forma (x,x).
R = {(1,1), (1,3), (2,2), (2,1), (3,3)} SÍ ES ANTISIMÉTRICO, ya que los casos en que sí hai simetría xRy y yRx son aquellos en que los dos términos son iguales - (1,1) y (2,2).
R = {(1,3), (2,1), (1,4)} SÍ ES ANTISIMÉTRICO: no hay ningún par con simetrías, con lo que la intersección de R y su inverso es el conjunto vacío.
4) Transitiva: una relación será transitiva si para todo trío x,y,z, si xRy y yRz, se sigue entonces que xRz (otra forma sería que R es el conjunto que incluye todas las composiciones de R con R tal que el resultado es un subconjunto de R). Partiendo del conjunto U = {1,2,3}
R = {(1,2), (2,3), (3,3)} NO ES TRANSITIVO. Si decidimos que x=1, y=2 y z=3, tenemos (1,2) y (2,3), pero no tenemos (como tendríamos que tener) (1,3).
R = {(1,2), (2,3), (1,3)} SÍ ES TRANSITIVO. Si decidimos lo mismo que en el caso previo, sólo tenemos un recorrido ternario: (1,2), (2,3), (1,3).
he hecho los ejercicios 1 y 2 de la unidad que trabajan relaciones lógicas. Seguramente los vuelva a hacer de nuevo 'a limpio' y los postee aquí, comentando los casos en que cometí errores.