Foundations of Mathematics - Tema 1

Muy ocupado con el trabajo. Como ya os ponía en la entrada anterior, he decidido aparcar la materia de Matemática Discreta e intentar centrarme en Lenguaje, aunque tampoco esté seguro de que vaya a tener el suficiente tiempo para esta. Para intentar complementarla y consolidarla mejor, he empezado también el libro de Ian Stewart y David Hall The Foundations of Mathematics, que cubre un espectro similar.

He hecho los ejercicios del tema 1, cuyas respuestas coloco aquí.

Priorizando

A estas alturas, me veo en la obligación de tomar una decisión desagradable que nunca había tenido que hacer con anterioridad. Estoy viendo que no voy a tener tiempo para preparar bien las dos materias en que me he matriculado este cuatrimestre, con lo que voy a tener que sacrificar una para septiembre.

Dado que tengo mucho más avanzado el libro de Lenguaje Matemático, va a ser Matemática Discreta la que deje de lado.

Para el año que viene tengo que calcular mejor los tiempos. Cada materia de las actuales requiere un mínimo de 2 horas de estudio diario, que en estos momentos apenas tengo (el año que viene tendré algo más). E imagino que asignaturas más difíciles requerirán aún más.

Con algo de suerte, y contando con la segunda convocatoria, espero poder aprobar las 3 asignaturas de este año. Si no es el caso, seguramente tendré que replantarme muy seriamente los estudios.

Autoexplicando cosas

He intentado acabar desde la última entrada el tema 3 de Lenguaje, pero me he visto atascado durante una semana por lo menos con la demostración que acabo de explicar a continuación, y que no era capaz de seguir. Luego de mucho pensar y una pequeña ayuda, he llegado a esto.

También tenía problemas con la de la siguiente página, que comprobaré esta noche si se han aclarado.

Progreso mucho más lento de lo que esperaba... A día de hoy, firmaba por aprobar con cualquier nota una de las dos materias que tengo este trimestre, y por sacar la otra en septiembre. Y veremos... Seguramente para el año tenga que restringirme a un ritmo más modesto de una asignatura por trimestre.

Como ya sabíamos que f(x) = f(x’) = y, y ahora hemos demostrado que x = x’, queda confirmado que f es una aplicación inyectiva. Como f es sobreyectiva e inyectiva, hemos demostrado que f es una aplicación biyectiva, el primer supuesto partiendo del segundo.

Relaciones Lógicas (3)

He estado muy atascado con los ejercicios 3 y 4 (sobre todo el 4), ya que son del tipo que no se sigue de modo sencillo y claro a partir de los ejemplos del texto. El mayor problema en este último caso fue entender correctamente qué significaba el conjunto {0,1}^8, ya que durante mucho tiempo (como se puede ver el los ejercicios 'incorrectos' que subo de 4) pensé que eran 8 números de 8 dígitos cada uno, unos y ceros, en vez de un único número.

Otro problema importante lo tuve con el último apartado de ese ejercicio, al planteárseme una alternativa entre dos opciones 'o' que justificaban la relación. No tenía claro a cual de las dos atender, y/o a qué reducir la relación. Por lo que me ha aclarado una profesora, si cualquiera de las dos opciones tiene una propiedad, se puede decir que la relación entera tiene dicha propiedad:

Página 1, 2, 3, 4 y ejercicio 4 (rehecho).

Relaciones lógicas (2)

Aquí van las versiones a limpio de los ejercicios 1 y 2. Los he hecho 'de nuevo' desde 0, aunque claramente me acordaba de las cosas, incluyendo los dos errores que cometí la primera vez en 1, cuando pensé que d) no era antisimétrico (porque no tenía un par (x,x) satisfaciendo xRy e yRx) y cuando (por un erro de cálculo) pensé que encontrara un contraejemplo demostrando que f) no era transitiva. A respecto de esta última relación, creo que encontré una prueba que es diferente a la de las soluciones del libro y válida.

En el ejercicio 2, los argumentos que uso a veces para justificar la respuesta son diferentes a los del libro; me queda pendiente leerlos con calma y ver que no haya contradicción (y que los entienda).

Relaciones Lógicas

En el comienzo del tema 3 de Lenguaje Matemático se habla sobre relaciones lógicas; aunque no se explicite, la impresión que me dan es que son una especie de precursores o de forma primitiva de las funciones matemáticas, simplemente vistiendo ropaje de teoría de conjuntos. Se explica que las relaciones pueden ser de 4 tipos (en mis propias palabras, intentando no consultar el libro).

Primero tenemos que asumir que R es una relación incluyendo pares (x,y) con x e y provenientes de, digamos, un conjunto U (habitualmente, ese conjunto sería R, el de los números reales, y los pares resultantes de la relación provenientes del producto RxR).

1) Reflexiva: una relación será reflexiva si para todo x perteneciente a U existe la relación xRx. Viéndolo bajo la forma de conjuntos, el conjunto R es reflexivo si contiene todos los pares (x,x) posibles a partir de los elementos de U. Un par de ejemplos, partiendo del conjunto U = {1,2,3,4}:

R = {(1,1), (1,3), (2,2), (2,1), (3,3)} NO ES REFLEXIVO: le faltaría incluír el par (4,4).

R = {1,1), (1,3), (2,2), (3,3), (3,4)} SÍ ES REFLEXIVO: tiene todos los pares (x,x) posibles.

2) Simétrica: una relación será simétrica si para todo par x, y perteneciente a U, si existe la relación xRy, entonces existe también la relación yRx. Técnicamente, se puede plantear como la afirmación de que si un conjunto R es simétrico, entonces contendrá a su inverso como subconjunto. De nuevo, partiendo del conjunto U = {1,2,3,4}:

R = {(1,2), (2,1), (3,1)} NO ES SIMÉTRICO: le faltaría incluír el par (1,3).  

R = {(1,2), (2,1), (3,1), (1,3)} SÍ ES SIMÉTRICO. Para cada par xy del conjunto, existe un par yx. Nótese que no hace falta (como con la propiedad reflexiva) incluír todos los pares posibles del conjunto U; sólo para aquellos pares que están en R.

3) Antisimétrica: una relación será antisimétrica si para todo par x, y perteneciente a U, si hay algún caso en que xRy y yRx (no tiene porqué haberlos), necesariamente será porque x=y. No es posible que se de la situación con x e y diferentes. Técnicamente se plantea que la intersección de R y su recíproco serían un subconjunto del conjunto reflexivo (o sea, pares x,x). Partiendo del conjunto U = {1,2,3,4}:

R = {(1,2), (2,1), (3,1)} NO ES ANTISIMÉTRICO: ya que tenemos un caso por lo menos donde la intersección de R y su recíproco no es de la forma (x,x).

R = {(1,1), (1,3), (2,2), (2,1), (3,3)} SÍ ES ANTISIMÉTRICO, ya que los casos en que sí hai simetría xRy y yRx son aquellos en que los dos términos son iguales - (1,1) y (2,2).

R = {(1,3), (2,1), (1,4)} SÍ ES ANTISIMÉTRICO: no hay ningún par con simetrías, con lo que la intersección de R y su inverso es el conjunto vacío.

4) Transitiva: una relación será transitiva si para todo trío x,y,z, si xRy y yRz, se sigue entonces que xRz  (otra forma sería que R es el conjunto que incluye todas las composiciones de R con R tal que el resultado es un subconjunto de R). Partiendo del conjunto U = {1,2,3}

R = {(1,2), (2,3), (3,3)} NO ES TRANSITIVO. Si decidimos que x=1, y=2 y z=3, tenemos (1,2) y (2,3), pero no tenemos (como tendríamos que tener) (1,3).

R = {(1,2), (2,3), (1,3)} SÍ ES TRANSITIVO. Si decidimos lo mismo que en el caso previo, sólo tenemos un recorrido ternario: (1,2), (2,3), (1,3).

he hecho los ejercicios 1 y 2 de la unidad que trabajan relaciones lógicas. Seguramente los vuelva a hacer de nuevo 'a limpio' y los postee aquí, comentando los casos en que cometí errores.

Matemática Discreta - ejercicios del tema 1.2

En general, os 5 ejercicios eran asequibles. En algunos casos, ni siquiera tuve que mirar atrás para ver cómo se hacían por el ejemplo del libro. En cambio, el 3 me atascó durante día y pico, y tuve que buscar en la red alguna pista, ya que al contrario que otros, no tenía un ejemplo directo en el que modelarse en la sección 1.2. En el 4 conseguí el resultado correcto, pero pensé que tenía que consultar los 29 primeros primos, en vez de los 29 primeros números, así que hice mucho trabajo redundante. El 5 es fácil siguiendo el modelo pero haciéndolo abstracto; la primera vez tuve que ir viendo paso a paso el ejemplo del libro, y 'traduciéndolo' a este caso. La segunda vez lo hice automáticamente.

Para cada entero n > 0 existen n números compuestos positivos y consecutivos

Seguimos a paso de caracol en el libro de Matemática Discreta. Esta vuelta lo que me ha atascado ha sido la siguiente demostración, que voy a intentar explicarme a mí mismo sin consultarla.

En páginas anteriores, el libro ha ido desmenuzando algunos datos sobre números primos, como que hay un número infinito de éstos, o que hay infinitos números primos con ciertas propiedades (como estar separados entre sí ciertas distancias). La siguiente demostración es un poco 'al revés': consiste en demostrar que aunque los primos son infinitos, existen bloques de números consecutivos sin primos tan grandes como se desee. De hecho, el tamaño de estos bloques ininterrumpidos de números compuestos puede ser el de cualquier número natural: 1, 2, 3, 100, 1000, 1000000... .  La demostración, además, genera una 'fórmula' que permite no sólo demostrar que existen, sino producir un ejemplo (es una prueba 'constructiva').

El primer paso consiste en utilizar factoriales (n!), que tienen la agradable propiedad de que cada uno contiene a TODOS los números anteriores a el en su factorización. Así, 3! = 3x2x1, y 6! = 6x5x4x3x2x1.

Para la prueba necesitamos que nos números sean consecutivos, así que pensemos en la siguiente serie, con n ≥ 1:

(n+1)! + 2, (n+1)!+3, (n+1)!+4 ... (n+1)+n+1

Es evidente que los números que genera esta serie son consecutivos (y positivos). ¿Cómo podemos saber si son compuestos ( = divisibles por algún número diferente de 1 y de sí mismos)?

Cojamos, por ejemplo, n=3. Entonces la serie se vuelve:

(4)! + 2, (4)!+3, (4!)+4

Sabemos que 4! = 4x3x2x1. Entonces 2 divide a 4! y (evidentemente), 2 se divide a sí mismo, así que 2 divide a (4)! + 2, que es un número compuesto. El siguiente, (4)!+3, es claramente el sucesor del anterior; 3 lo divide, e igualmente se divide a sí mismo. Igualmente, el siguiente, (4!)+4 es sucesor del anterior, y sus dos sumandos son divisibles por cuatro. Si los calculamos, hemos generado tres números consecutivos, 26, 27 y 28, que son todos compuestos (el siguiente, 29, es primo).

Es trivial constatar que la fórmula es ampliable infinitamente, y que funcionará con n más grandes por el mismo motivo (el factorial siempre incluirá entre sus factores a todos los números anteriores, y nos valdrá hasta (n+1)! + n + 1 para cualquier n > 1; y todos los sumandos acompañantes y menores que (n+1) serán divisibles por sí mismos). Si n = 3 nos generaba 3 compuestos consecutivos, n = 1 nos genera 1 (4), n = 2 nos genera 2 (8, 9), 4 nos genera 4 (120, 121, 122, 123, 124) y así sucesivamente.

Incidentalmente, a veces el siguiente(s) en la secuencia también son compuestos (en el último caso, 125 y 126 lo son), pero la fórmula sólo nos los garantiza para el n escogido.

Este demostración me tuvo día y medio atascado; sospecho que porque esperaba inconscientemente un mismo divisor para todos ellos.

Lenguaje matemático - ejercicios del tema 2 (3)

Aquí van.

Lema de Euclides y sus corolarios

Vuelvo a pelear con el libro de Matemática Discreta, y avanzando a paso de caracol. En una reciente videoconferencia introduciendo el curso, el profesor (y uno de los autores del volumen) Emilio Bujalance deja claro que hay que avanzar lenta y metódicamente con el libro (no es una lectura como la de una novela; hay que pararse, pensar, intentar realmente entender lo que se lee), pero temo que con este grado de dificultad, necesitaría todo el curso y por lo menos 2-3 horas diarias para poder completarlo. Ya veremos...

Hoy me proponía avanzar muy mucho en la sección 1.2 dedicada a los números primos, pero ya entre las primeras páginas, me topé con dificultades con un corolario del Lema de Euclides que me llevó un par de horas y algunas consultas poder comprender. Voy a intentar explicármelo con mis propias palabras como posible recordatorio para el futuro y para memorizarlo mejor.

La lema (¿el lema? ¿Cual es el género de esta palabra?), inserta en en contexto de temas de primalidad y co-primalidad, viene a formular lo siguiente:

-Dados 3 números enteros, a, b, c...

-Si a y c son coprimos entre sí...

-Y c divide al producto de bc...

ENTONCES, c necesariamente divide a b.

A priori, esto parece de sentido común (seguramente porque estoy aplicando el conocimiento informal de estudiante, frente a lo que se explicará rigurosamente más adelante en el libro, a la factorización de números en sus constituyentes primos). El libro lo demuestra de un modo bastante sencillo: si a y c son coprimos (=su mayor divisor común es 1), luego por la Identidad de Bezout, pueden representarse de la forma ax + cy = 1. Si multiplicamos ambos lados por b, tenemos bax + bcy = b. Es obvio que c divide a bcy; por el tercer punto que pusimos arriba, como c divide a ab, dividirá a bax; si divide a cada uno de los sumandos de la izquierda, tiene que poder dividir la igualdad de la derecha, y c divide a b.

(Incidentalmente, conviene dejar aclaradas las definiciones de primalidad y coprimalidad: un número primo es un entero mayor que 1 que sólo es divisible por sí mismo y por 1; números coprimos son aquellos que, sean o no primos, no comparten divisores comunes más allá del 1).

Los problemas me vinieron con un coralario de esta lema. El corolario establecía la siguiente identidad:

-Sea p un número entero mayor que 1...

-Si para TODAS las parejas de números enteros a, b cuyo producto, ab es divisible por p...

-P divide a uno (o a ambos) factores, esto es lo mismo que decir que...

ENTONCES p es un número primo (de hecho, esta puede ser una definición alternativa de número primo).

El problema que tuve fue básicamente que no percibía con claridad que esta relación entre p, a y b sólo era válida para TODAS las parejas. En efecto, es fácil topar números p mayores que 1 que dividen a un producto de números y a cada uno de los factores sin que p sea primo (por ejemplo, p = 4, a = 12, c = 16), pero si tenemos que tener en cuenta la totalidad de parejas a y b cuyo producto es divisible por p, entonces es fácil encontrar parejas donde este p no podría dividir a los factores: los casos en que los factores son menores que p. En nuestro ejemplo, p = 4, a = 2, b = 2. Si p es primo esto no pasará, porque tendremos al primo entre los factores (abierta o soterradamente) de a y/o de b).

El segundo corolario era más sencillo, y simplemente expandía esta regra de dos números, a y b, a una serie tan extensa como se quiera.

Lenguaje matemático - ejercicios del tema 2 (2)

Por fin he acabado los 24 ejercicios: son 13 páginas por las dos caras al final. En algunos he tenido que consultar la parte de las soluciones simplemente para entender qué es lo que se me pedía, pero en la mayoría no ha hecho falta. Algunos han sido relativamente fáciles, aunque en los casos más frecuentes, he tenido que estrujar el cerebro.

Los que más problemas me dan suelen ser los de 'demostrar'. Intentaré quizás mañana o pasado reconstruír uno de ellos, y ver si soy capaz.

¿Planes para los próximos días? Voy a volver mañana al libro de Discreta, intentando avanzar bien en la sección 1.2 (Números Primos). Por lo que toca a Lenguaje, voy a procurar ir haciendo los ejercicios de final de tema al mismo tiempo que la lectura de las partes de éste, para evitar eternizarme y tener todo más fresco.

Lenguaje matemático - ejercicios del tema 2 (1)

El tema dos presenta la friolera de 24 (!?) ejercicios, que además son densos, de meditar y pensar mucho en la mayoría de los casos. Voy avanzando a paso de caracol. En estos momentos, he acabado hasta el 11, y confío (quizás optimista de más) en acabar todos en el puente que se nos avecina.

Enzarzado

Seguimos avanzando lentamente - mucho más lentamente de lo debiera, pero todas las cosas me están llevando muchísimo tiempo.

Estoy con los ejercicios del tema 2 del libro de Lenguaje Matemático, donde voy por el 10 (de 24). Varios me han dado importantes quebraderos de cabeza que comentaré cuando suba las hojas con las respuestas. 

En lo que toca a Matemática Discreta, tengo el libro parado luego de acabar la sección 1.1 hasta que acabe los ejercicios de Lenguaje. Para ir haciendo algo, he estado mirando los vídeos con ejercicios resueltos que hay en la plataforma. El primero, que ejemplifica el uso de Algoritmo de Euclides, me resultó muy fácil y me ha permitido asimilar la mecánica de esta tarea, que luego realicé con éxito en el libro de texto. El segundo vídeo incluye un ejercicio bastante difícil y sin ejemplo equivalente en el libro, empleando aritmética modular para descomponer un número en otros tres. No sería capaz de hacerlo yo sólo, pero he podido seguir los pasos de la descripción, y viendo el vídeo un par de veces más creo que sí podría afrontar este tipo de ejercicio. El tercer vídeo ponía un ejercicio que emplea aritmética modular y divisibilidad, y me resultó bastante fácil. Aquí cuelgo las notas.

Matemática Discreta - ejercicios del tema 1.1

Son sólo siete, pero algunos fueron bastante durillos de pelar y me requirieron mucho tiempo de pensar y de concentración. Me preocupa un poco lo lento que progreso con este libro de texto.

Ningún número n^2+1 es múltiplo de 7

Para empezar la prueba, como en tantas otras, comenzamos suponiendo lo contrario de lo que se quiere probar hasta llegar a una contradicción.

1) Asumimos, entonces, que existe un número n tal que n^2+1 es un múltiplo de 7, por lo que es equivalente a 7q: n^2+1 = 7q

Hay varias formas de manipular algebraicamente esta igualdad, pero para manipulaciones posteriores, lo ideal será una forma del modelo general aq+r. Para hacer eso, primero aislamos el cuadrado en un lado de la igualdad: n^2 = 7q -1; ese -1 puede cambiarse por un equivalente -7 + 6: 7q -7+6; factorizando el siete tenemos 7(q-1)+6; y finalmente, n^2 = 7(q-1)+6.

2) Gracias a la transformación que hemos hecho, resulta evidente ver que n^2 MOD 7 = 6. 

3) Necesitamos antes de proseguir aclarar una serie de pormenores que nos serán útiles en la siguiente parte de la prueba. El primero es que n MOD 7 = (n MOD 7) MOD 7. Esto parecería trivial (sea cual sea n, la primera operación del módulo lo transforma en un número <7; sucesivas iteraciones no alterarán esto: al ya estar (n MOD 7) en su 'forma mínima', el repetir la operación MOD lo mantiene igual), pero será útil. Igualmente, n^2 MOD 7 = (n^2 MOD 7) MOD 7.

El otro pormenor que necesitamos recordar es que, por propiedades modulares, si a MOD n = c MOD n y b MOD n = d MOD n, entonces (ab) MOD n = (cd) MOD n.

4) Básicamente, vamos a aplicar la última igualdad, luego de fijar las siguientes equivalencias:

a = n

b = n MOD 7

c = n

d = n MOD 7

Haciendo la multiplicación e igualación pertinente, tenemos que (n x n) MOD 7 = [(n MOD 7) x (n MOD 7)] MOD 7. Esto es igual a n^2 MOD 7 = (n MOD 7)^2 MOD 7.

5) Parece que no hemos avanzado mucho, pero esta igualdad es clave. Ya habíamos bisto por el paso 2 que la parte derecha de la igualdad es igual a 6. Ahora tenemos una parte derecha de la igualdad donde sólo tenemos que comprobar todos los valores posibles para n MOD 7 (0,1,2,3,4,5,6) y luego elevarlos al cuadrado. Si alguno de ellos, luego de aplicarle MOD 7, es 6, entonces nuestra asunción es verdadera. Lo comprobamos:

(0 MOD 7)^2 = 0^2 = 0 NO 

(1 MOD 7)^2 = 1^2 = 1 NO 

(2 MOD 7)^2 = 2^2 = 4 NO 

(3 MOD 7)^2 = 3^2 = (9) 2 NO 

(4 MOD 7)^2 = 4^2 = (16) 2 NO 

(5 MOD 7)^2 = 5^2 = (25) 4 NO

(6 MOD 7)^2 = 6^2 = (36) 1 NO  

6) Conclusión: ya que hemos llegado a una contradicción, y la mitad derecha de la igualdad no es 6 en ningún caso, nuestra asunción era falsa, con lo que queda demostrado que ningún número de la forma n^2+1 puede ser múltiplo de 7.

Autoexplicando cosas

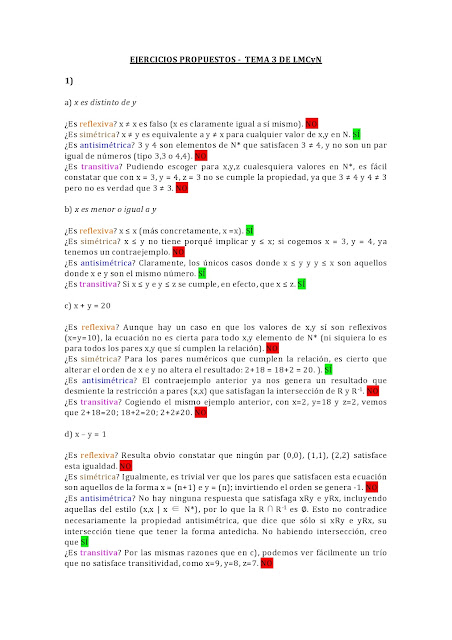
Como creo que ya he comentado, el libro de Matemática Discreta es muy denso y muy difícil, siguiendo el patrón de los libros de matemática avanzada (Descripción, Propiedades, Demostración, Corolarios, Ejemplos). Dado que muchos pasos menores y/o intermedios no se especifican, estoy intentado autoexplicármelos en detalle mediante notas.

Aquí van dos de las cosas que me he autoexplicado. Una de ellas se refiere a valores absolutos. Lo que hay que demostrar es que  |a| ≤ b si y sólo si a ≤ b y -a ≤ b (ver imagen adjunta).

El siguiente (en este caso lo trabajé en documento doc) es el algoritmo de la división, que va así:

Nos son dados los siguientes 4 números, con las siguientes propiedades:

a ∈Z

b ∈N

q ∈Z

r ∈Z

Afirmamos lo siguiente: que a = bq + rcon 0 ≤ r < b, y que q y r son únicos.

¿Qué quiere decir esta afirmación? Pues que cualquier número entero es descomponible en otros dos números, uno natural (1, 2, 3…) multiplicado por otro entero, y produciendo también un resto que puede ir desde 0 hasta b-1.

Se dice que q y r son únicos en el sentido de que si fijamos unos a y b concretos (por ejemplo, a=12 y b=6, entonces sólo un número puede ser q (2) y sólo un número puede ser r (0).

¿Cómo lo demostramos?

PASO 1: partimos de los 4 números que hemos escogido. Vamos a acotar algo más sus propiedades, a mayores de indicar a qué clase de números pertenecen. Vamos a decidir que en la expresión bq, q sea el mayor múltiplo de b que sea menor o igual que a. Por ejemplo, en el ejemplo anterior, si a es 12 y b 6, ¿cual es el mayor múltiplo de 6 que se aproxima, o iguala 12, sin pasarlo? 6x1 = 6; 6x2 = 12. Es 2.

Otro ejemplo, para a=120 y b = 7. Por tanteo, probamos con 12, y nos sale 7x12= 84, muy bajo. Con 15 nos sale 7x15= 105; Con 17 nos sale 7x17 = 119. Es 17.

Por definición, es obvio que bq ≤ a < b(q+1). La parte de b(q+1) deriva de la definición; si bq es el mayor múltiplo igual o menor que a, entonces si añadimos 1 a q generamos otro número, (q+1), que va a ser más grande que a (en el último ejemplo previo, 7 x 18, por ejemplo, es 126, por encima de 120).

PASO 2: En la desigualdad anterior, vamos a restar bq a cada uno de sus elementos:

bq –bq ≤ a –bq  < b(q+1) –bq

Simplificando, nos queda que

0 ≤ a –bq < bq + b – bq

0 ≤ a –bq < b 

Volviendo a la expresión algebraica de la que queríamos partir, a = bq + r, una sencilla operación algebraica la transforma en r = a – bq. Sustituyendo en la desigualdad previa, resulta que

0 ≤ r < b 

Con lo cual hemos demostrado que se satisfacen parte de las condiciones iniciales.

PASO 3: Ahora nos toca demostrar la unicidad de q y r. Por la definición de la división en números enteros y por lo que acabamos de ver, sabemos que a = bq + r. Vamos a imaginar que la igualdad puede cumplirse con q_sy r_sdiferentes; o sea:

a = bq₁+ r₁= bq₂+ r₂, r₁ ≠r₂

Manipulando algebraicamente la igualdad bq₁+ r₁= bq₂+ r₂, r₁ podemos poner las bq_sen un lado y las r_sen el otro:

r₁- r₂ = bq₂ – bq₁

Y factorizamos el b común de la derecha y tenemos

r₁- r₂ = b(q₂ – q₁)

El producto de la derecha es interesante, porque por la definición de la división, sabemos que b | (r₁- r₂). Por la quinta propiedadde valores absolutos, sabemos que si a ≠0, b ≠0 y a | b, entonces |a| ≤ |b|. Aplicándolo a las variables con las que estamos trabajando, tendríamos que |b| ≤ |r₁- r₂ |

Por definición, sabemos que r tiene que ser 0 ≤ r < b. En este caso suponíamos la existencia de dos r_sno iguales. Cada una de ellas tendrá que cumplir con la misma propiedad, a saber:

0 ≤ r₁< b                               0 ≤ r₂< b

Pero si estas dos desigualdades son ciertas, tenemos la situación de que |b| (que es igual a b, ya que b ∉ N) es mayor que el valor absoluto de r₁- r₂. O sea:

|b| > |r₁- r₂ |

Lo cual entra en contradicción con lo que descubrimos unos párrafos más arriba, o sea:

|b| ≤ |r₁- r₂ |

Esta contradicción demuestra la falsedad de nuestro postulado sobre la posibilidad de q_s y r_s diferentes, lo cual quiere decir que por fuerza, q₁ = q₂ y r₁= r₂(otra forma de afirmar esto último es decir que su diferencia es 0, r₁- r₂= 0).

Lo anterior es válido en las condiciones que hemos formulado, pero ¿qué pasa si quisiésemos extenderlo de b ∈N a b ∈Z (excluyendo, obviamente, a b = 0 porque no se puede dividir por 0), y teniendo que pasar de b a |b| para evitar problemas con negativos? O sea:

a = bq + rcon 0 ≤ r < |b|

 Eso se soluciona con el siguiente corolario:

1) Para el caso b > 0, la demostración anterior ya nos vale.

2) Para el caso b < 0 : Si b es menor que 0, entonces su inverso, -b, es mayor que 0. Entonces, por el teorema anterior (que se aplicaba a todo número > 0) tenemos que

a = (-b)q’ + rcon 0 ≤ r < (-b)

Algebraicamente, podemos quitarle ese signo negativo a la b y pasárselo a q’:

a = b(-q’) + rcon 0 ≤ r < (-b)

Y el (-b) de final de la desigualdad podemos cambiarlo por |b| (que es igual a –b si b es <0, por definición de valor absoluto).

a = b(-q’) + rcon 0 ≤ r < |b|

Y ya está. –q’ si queremos podemos llamarlo q, y ya hemos vuelto a la forma inicial, añadiendo el valor absoluto para b:

a = bq + rcon 0 ≤ r < |b|

Igualmente, se cumpliría por las mismas reglas la unicidad de q y r por lo expuesto con anterioridad.