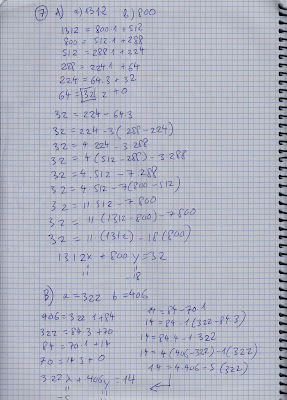Lenguaje matemático - ejercicios del tema 2 (1)

El tema dos presenta la friolera de 24 (!?) ejercicios, que además son densos, de meditar y pensar mucho en la mayoría de los casos. Voy avanzando a paso de caracol. En estos momentos, he acabado hasta el 11, y confío (quizás optimista de más) en acabar todos en el puente que se nos avecina.

Enzarzado

Seguimos avanzando lentamente - mucho más lentamente de lo debiera, pero todas las cosas me están llevando muchísimo tiempo.

Estoy con los ejercicios del tema 2 del libro de Lenguaje Matemático, donde voy por el 10 (de 24). Varios me han dado importantes quebraderos de cabeza que comentaré cuando suba las hojas con las respuestas. 

En lo que toca a Matemática Discreta, tengo el libro parado luego de acabar la sección 1.1 hasta que acabe los ejercicios de Lenguaje. Para ir haciendo algo, he estado mirando los vídeos con ejercicios resueltos que hay en la plataforma. El primero, que ejemplifica el uso de Algoritmo de Euclides, me resultó muy fácil y me ha permitido asimilar la mecánica de esta tarea, que luego realicé con éxito en el libro de texto. El segundo vídeo incluye un ejercicio bastante difícil y sin ejemplo equivalente en el libro, empleando aritmética modular para descomponer un número en otros tres. No sería capaz de hacerlo yo sólo, pero he podido seguir los pasos de la descripción, y viendo el vídeo un par de veces más creo que sí podría afrontar este tipo de ejercicio. El tercer vídeo ponía un ejercicio que emplea aritmética modular y divisibilidad, y me resultó bastante fácil. Aquí cuelgo las notas.

Matemática Discreta - ejercicios del tema 1.1

Son sólo siete, pero algunos fueron bastante durillos de pelar y me requirieron mucho tiempo de pensar y de concentración. Me preocupa un poco lo lento que progreso con este libro de texto.

Ningún número n^2+1 es múltiplo de 7

Para empezar la prueba, como en tantas otras, comenzamos suponiendo lo contrario de lo que se quiere probar hasta llegar a una contradicción.

1) Asumimos, entonces, que existe un número n tal que n^2+1 es un múltiplo de 7, por lo que es equivalente a 7q: n^2+1 = 7q

Hay varias formas de manipular algebraicamente esta igualdad, pero para manipulaciones posteriores, lo ideal será una forma del modelo general aq+r. Para hacer eso, primero aislamos el cuadrado en un lado de la igualdad: n^2 = 7q -1; ese -1 puede cambiarse por un equivalente -7 + 6: 7q -7+6; factorizando el siete tenemos 7(q-1)+6; y finalmente, n^2 = 7(q-1)+6.

2) Gracias a la transformación que hemos hecho, resulta evidente ver que n^2 MOD 7 = 6. 

3) Necesitamos antes de proseguir aclarar una serie de pormenores que nos serán útiles en la siguiente parte de la prueba. El primero es que n MOD 7 = (n MOD 7) MOD 7. Esto parecería trivial (sea cual sea n, la primera operación del módulo lo transforma en un número <7; sucesivas iteraciones no alterarán esto: al ya estar (n MOD 7) en su 'forma mínima', el repetir la operación MOD lo mantiene igual), pero será útil. Igualmente, n^2 MOD 7 = (n^2 MOD 7) MOD 7.

El otro pormenor que necesitamos recordar es que, por propiedades modulares, si a MOD n = c MOD n y b MOD n = d MOD n, entonces (ab) MOD n = (cd) MOD n.

4) Básicamente, vamos a aplicar la última igualdad, luego de fijar las siguientes equivalencias:

a = n

b = n MOD 7

c = n

d = n MOD 7

Haciendo la multiplicación e igualación pertinente, tenemos que (n x n) MOD 7 = [(n MOD 7) x (n MOD 7)] MOD 7. Esto es igual a n^2 MOD 7 = (n MOD 7)^2 MOD 7.

5) Parece que no hemos avanzado mucho, pero esta igualdad es clave. Ya habíamos bisto por el paso 2 que la parte derecha de la igualdad es igual a 6. Ahora tenemos una parte derecha de la igualdad donde sólo tenemos que comprobar todos los valores posibles para n MOD 7 (0,1,2,3,4,5,6) y luego elevarlos al cuadrado. Si alguno de ellos, luego de aplicarle MOD 7, es 6, entonces nuestra asunción es verdadera. Lo comprobamos:

(0 MOD 7)^2 = 0^2 = 0 NO 

(1 MOD 7)^2 = 1^2 = 1 NO 

(2 MOD 7)^2 = 2^2 = 4 NO 

(3 MOD 7)^2 = 3^2 = (9) 2 NO 

(4 MOD 7)^2 = 4^2 = (16) 2 NO 

(5 MOD 7)^2 = 5^2 = (25) 4 NO

(6 MOD 7)^2 = 6^2 = (36) 1 NO  

6) Conclusión: ya que hemos llegado a una contradicción, y la mitad derecha de la igualdad no es 6 en ningún caso, nuestra asunción era falsa, con lo que queda demostrado que ningún número de la forma n^2+1 puede ser múltiplo de 7.

Autoexplicando cosas

Como creo que ya he comentado, el libro de Matemática Discreta es muy denso y muy difícil, siguiendo el patrón de los libros de matemática avanzada (Descripción, Propiedades, Demostración, Corolarios, Ejemplos). Dado que muchos pasos menores y/o intermedios no se especifican, estoy intentado autoexplicármelos en detalle mediante notas.

Aquí van dos de las cosas que me he autoexplicado. Una de ellas se refiere a valores absolutos. Lo que hay que demostrar es que  |a| ≤ b si y sólo si a ≤ b y -a ≤ b (ver imagen adjunta).

El siguiente (en este caso lo trabajé en documento doc) es el algoritmo de la división, que va así:

Nos son dados los siguientes 4 números, con las siguientes propiedades:

a ∈Z

b ∈N

q ∈Z

r ∈Z

Afirmamos lo siguiente: que a = bq + rcon 0 ≤ r < b, y que q y r son únicos.

¿Qué quiere decir esta afirmación? Pues que cualquier número entero es descomponible en otros dos números, uno natural (1, 2, 3…) multiplicado por otro entero, y produciendo también un resto que puede ir desde 0 hasta b-1.

Se dice que q y r son únicos en el sentido de que si fijamos unos a y b concretos (por ejemplo, a=12 y b=6, entonces sólo un número puede ser q (2) y sólo un número puede ser r (0).

¿Cómo lo demostramos?

PASO 1: partimos de los 4 números que hemos escogido. Vamos a acotar algo más sus propiedades, a mayores de indicar a qué clase de números pertenecen. Vamos a decidir que en la expresión bq, q sea el mayor múltiplo de b que sea menor o igual que a. Por ejemplo, en el ejemplo anterior, si a es 12 y b 6, ¿cual es el mayor múltiplo de 6 que se aproxima, o iguala 12, sin pasarlo? 6x1 = 6; 6x2 = 12. Es 2.

Otro ejemplo, para a=120 y b = 7. Por tanteo, probamos con 12, y nos sale 7x12= 84, muy bajo. Con 15 nos sale 7x15= 105; Con 17 nos sale 7x17 = 119. Es 17.

Por definición, es obvio que bq ≤ a < b(q+1). La parte de b(q+1) deriva de la definición; si bq es el mayor múltiplo igual o menor que a, entonces si añadimos 1 a q generamos otro número, (q+1), que va a ser más grande que a (en el último ejemplo previo, 7 x 18, por ejemplo, es 126, por encima de 120).

PASO 2: En la desigualdad anterior, vamos a restar bq a cada uno de sus elementos:

bq –bq ≤ a –bq  < b(q+1) –bq

Simplificando, nos queda que

0 ≤ a –bq < bq + b – bq

0 ≤ a –bq < b 

Volviendo a la expresión algebraica de la que queríamos partir, a = bq + r, una sencilla operación algebraica la transforma en r = a – bq. Sustituyendo en la desigualdad previa, resulta que

0 ≤ r < b 

Con lo cual hemos demostrado que se satisfacen parte de las condiciones iniciales.

PASO 3: Ahora nos toca demostrar la unicidad de q y r. Por la definición de la división en números enteros y por lo que acabamos de ver, sabemos que a = bq + r. Vamos a imaginar que la igualdad puede cumplirse con q_sy r_sdiferentes; o sea:

a = bq₁+ r₁= bq₂+ r₂, r₁ ≠r₂

Manipulando algebraicamente la igualdad bq₁+ r₁= bq₂+ r₂, r₁ podemos poner las bq_sen un lado y las r_sen el otro:

r₁- r₂ = bq₂ – bq₁

Y factorizamos el b común de la derecha y tenemos

r₁- r₂ = b(q₂ – q₁)

El producto de la derecha es interesante, porque por la definición de la división, sabemos que b | (r₁- r₂). Por la quinta propiedadde valores absolutos, sabemos que si a ≠0, b ≠0 y a | b, entonces |a| ≤ |b|. Aplicándolo a las variables con las que estamos trabajando, tendríamos que |b| ≤ |r₁- r₂ |

Por definición, sabemos que r tiene que ser 0 ≤ r < b. En este caso suponíamos la existencia de dos r_sno iguales. Cada una de ellas tendrá que cumplir con la misma propiedad, a saber:

0 ≤ r₁< b                               0 ≤ r₂< b

Pero si estas dos desigualdades son ciertas, tenemos la situación de que |b| (que es igual a b, ya que b ∉ N) es mayor que el valor absoluto de r₁- r₂. O sea:

|b| > |r₁- r₂ |

Lo cual entra en contradicción con lo que descubrimos unos párrafos más arriba, o sea:

|b| ≤ |r₁- r₂ |

Esta contradicción demuestra la falsedad de nuestro postulado sobre la posibilidad de q_s y r_s diferentes, lo cual quiere decir que por fuerza, q₁ = q₂ y r₁= r₂(otra forma de afirmar esto último es decir que su diferencia es 0, r₁- r₂= 0).

Lo anterior es válido en las condiciones que hemos formulado, pero ¿qué pasa si quisiésemos extenderlo de b ∈N a b ∈Z (excluyendo, obviamente, a b = 0 porque no se puede dividir por 0), y teniendo que pasar de b a |b| para evitar problemas con negativos? O sea:

a = bq + rcon 0 ≤ r < |b|

 Eso se soluciona con el siguiente corolario:

1) Para el caso b > 0, la demostración anterior ya nos vale.

2) Para el caso b < 0 : Si b es menor que 0, entonces su inverso, -b, es mayor que 0. Entonces, por el teorema anterior (que se aplicaba a todo número > 0) tenemos que

a = (-b)q’ + rcon 0 ≤ r < (-b)

Algebraicamente, podemos quitarle ese signo negativo a la b y pasárselo a q’:

a = b(-q’) + rcon 0 ≤ r < (-b)

Y el (-b) de final de la desigualdad podemos cambiarlo por |b| (que es igual a –b si b es <0, por definición de valor absoluto).

a = b(-q’) + rcon 0 ≤ r < |b|

Y ya está. –q’ si queremos podemos llamarlo q, y ya hemos vuelto a la forma inicial, añadiendo el valor absoluto para b:

a = bq + rcon 0 ≤ r < |b|

Igualmente, se cumpliría por las mismas reglas la unicidad de q y r por lo expuesto con anterioridad.

Parte de guerra - 15 de Octubre

Voy prosiguiendo muy lentamente con las dos materias en que estoy matriculado este trimestre: Matemática Discreta y Lenguaje Matemático, Conjuntos y Números. Al margen de esto, también estoy con otras lecturas matemáticas (un libro divulgativo sobre fractales y entradas del Princeton Companion to Mathematics).

En Lenguaje he acabo la relectura del tema 2, que me ha quedado bastante máis claro, y me quedarían hacer sus ejercicios, que cuento con colgar aquí en no máis de una semana.

En Discreta mi progreso ha sido mucho más lento (aunque lo empecé más recientemente). Es un libro matemáticamente 'duro', en el que el modelo que se aplica es el de definición, propiedades, demostración y ejemplos. No es problemático sólo este carácter espartano: las demostraciones se comen algunos pasos (seguramente triviales para los autores del libro, pero no para mí). Luego de llegar a la Identidad de Bezout (antes de acabar la sección 1.1), decidí volver a empezar desde 0. Veremos si ahora vamos mejor...