Relaciones Lógicas (3)

He estado muy atascado con los ejercicios 3 y 4 (sobre todo el 4), ya que son del tipo que no se sigue de modo sencillo y claro a partir de los ejemplos del texto. El mayor problema en este último caso fue entender correctamente qué significaba el conjunto {0,1}^8, ya que durante mucho tiempo (como se puede ver el los ejercicios 'incorrectos' que subo de 4) pensé que eran 8 números de 8 dígitos cada uno, unos y ceros, en vez de un único número.

Otro problema importante lo tuve con el último apartado de ese ejercicio, al planteárseme una alternativa entre dos opciones 'o' que justificaban la relación. No tenía claro a cual de las dos atender, y/o a qué reducir la relación. Por lo que me ha aclarado una profesora, si cualquiera de las dos opciones tiene una propiedad, se puede decir que la relación entera tiene dicha propiedad:

Página 1, 2, 3, 4 y ejercicio 4 (rehecho).

Relaciones lógicas (2)

Aquí van las versiones a limpio de los ejercicios 1 y 2. Los he hecho 'de nuevo' desde 0, aunque claramente me acordaba de las cosas, incluyendo los dos errores que cometí la primera vez en 1, cuando pensé que d) no era antisimétrico (porque no tenía un par (x,x) satisfaciendo xRy e yRx) y cuando (por un erro de cálculo) pensé que encontrara un contraejemplo demostrando que f) no era transitiva. A respecto de esta última relación, creo que encontré una prueba que es diferente a la de las soluciones del libro y válida.

En el ejercicio 2, los argumentos que uso a veces para justificar la respuesta son diferentes a los del libro; me queda pendiente leerlos con calma y ver que no haya contradicción (y que los entienda).

Relaciones Lógicas

En el comienzo del tema 3 de Lenguaje Matemático se habla sobre relaciones lógicas; aunque no se explicite, la impresión que me dan es que son una especie de precursores o de forma primitiva de las funciones matemáticas, simplemente vistiendo ropaje de teoría de conjuntos. Se explica que las relaciones pueden ser de 4 tipos (en mis propias palabras, intentando no consultar el libro).

Primero tenemos que asumir que R es una relación incluyendo pares (x,y) con x e y provenientes de, digamos, un conjunto U (habitualmente, ese conjunto sería R, el de los números reales, y los pares resultantes de la relación provenientes del producto RxR).

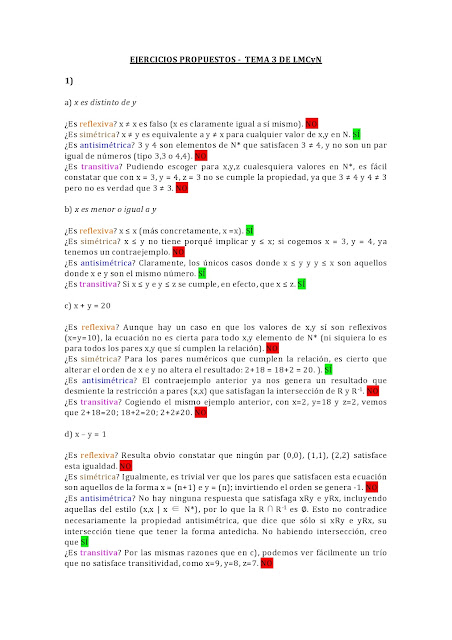
1) Reflexiva: una relación será reflexiva si para todo x perteneciente a U existe la relación xRx. Viéndolo bajo la forma de conjuntos, el conjunto R es reflexivo si contiene todos los pares (x,x) posibles a partir de los elementos de U. Un par de ejemplos, partiendo del conjunto U = {1,2,3,4}:

R = {(1,1), (1,3), (2,2), (2,1), (3,3)} NO ES REFLEXIVO: le faltaría incluír el par (4,4).

R = {1,1), (1,3), (2,2), (3,3), (3,4)} SÍ ES REFLEXIVO: tiene todos los pares (x,x) posibles.

2) Simétrica: una relación será simétrica si para todo par x, y perteneciente a U, si existe la relación xRy, entonces existe también la relación yRx. Técnicamente, se puede plantear como la afirmación de que si un conjunto R es simétrico, entonces contendrá a su inverso como subconjunto. De nuevo, partiendo del conjunto U = {1,2,3,4}:

R = {(1,2), (2,1), (3,1)} NO ES SIMÉTRICO: le faltaría incluír el par (1,3).  

R = {(1,2), (2,1), (3,1), (1,3)} SÍ ES SIMÉTRICO. Para cada par xy del conjunto, existe un par yx. Nótese que no hace falta (como con la propiedad reflexiva) incluír todos los pares posibles del conjunto U; sólo para aquellos pares que están en R.

3) Antisimétrica: una relación será antisimétrica si para todo par x, y perteneciente a U, si hay algún caso en que xRy y yRx (no tiene porqué haberlos), necesariamente será porque x=y. No es posible que se de la situación con x e y diferentes. Técnicamente se plantea que la intersección de R y su recíproco serían un subconjunto del conjunto reflexivo (o sea, pares x,x). Partiendo del conjunto U = {1,2,3,4}:

R = {(1,2), (2,1), (3,1)} NO ES ANTISIMÉTRICO: ya que tenemos un caso por lo menos donde la intersección de R y su recíproco no es de la forma (x,x).

R = {(1,1), (1,3), (2,2), (2,1), (3,3)} SÍ ES ANTISIMÉTRICO, ya que los casos en que sí hai simetría xRy y yRx son aquellos en que los dos términos son iguales - (1,1) y (2,2).

R = {(1,3), (2,1), (1,4)} SÍ ES ANTISIMÉTRICO: no hay ningún par con simetrías, con lo que la intersección de R y su inverso es el conjunto vacío.

4) Transitiva: una relación será transitiva si para todo trío x,y,z, si xRy y yRz, se sigue entonces que xRz  (otra forma sería que R es el conjunto que incluye todas las composiciones de R con R tal que el resultado es un subconjunto de R). Partiendo del conjunto U = {1,2,3}

R = {(1,2), (2,3), (3,3)} NO ES TRANSITIVO. Si decidimos que x=1, y=2 y z=3, tenemos (1,2) y (2,3), pero no tenemos (como tendríamos que tener) (1,3).

R = {(1,2), (2,3), (1,3)} SÍ ES TRANSITIVO. Si decidimos lo mismo que en el caso previo, sólo tenemos un recorrido ternario: (1,2), (2,3), (1,3).

he hecho los ejercicios 1 y 2 de la unidad que trabajan relaciones lógicas. Seguramente los vuelva a hacer de nuevo 'a limpio' y los postee aquí, comentando los casos en que cometí errores.

Matemática Discreta - ejercicios del tema 1.2

En general, os 5 ejercicios eran asequibles. En algunos casos, ni siquiera tuve que mirar atrás para ver cómo se hacían por el ejemplo del libro. En cambio, el 3 me atascó durante día y pico, y tuve que buscar en la red alguna pista, ya que al contrario que otros, no tenía un ejemplo directo en el que modelarse en la sección 1.2. En el 4 conseguí el resultado correcto, pero pensé que tenía que consultar los 29 primeros primos, en vez de los 29 primeros números, así que hice mucho trabajo redundante. El 5 es fácil siguiendo el modelo pero haciéndolo abstracto; la primera vez tuve que ir viendo paso a paso el ejemplo del libro, y 'traduciéndolo' a este caso. La segunda vez lo hice automáticamente.

Para cada entero n > 0 existen n números compuestos positivos y consecutivos

Seguimos a paso de caracol en el libro de Matemática Discreta. Esta vuelta lo que me ha atascado ha sido la siguiente demostración, que voy a intentar explicarme a mí mismo sin consultarla.

En páginas anteriores, el libro ha ido desmenuzando algunos datos sobre números primos, como que hay un número infinito de éstos, o que hay infinitos números primos con ciertas propiedades (como estar separados entre sí ciertas distancias). La siguiente demostración es un poco 'al revés': consiste en demostrar que aunque los primos son infinitos, existen bloques de números consecutivos sin primos tan grandes como se desee. De hecho, el tamaño de estos bloques ininterrumpidos de números compuestos puede ser el de cualquier número natural: 1, 2, 3, 100, 1000, 1000000... .  La demostración, además, genera una 'fórmula' que permite no sólo demostrar que existen, sino producir un ejemplo (es una prueba 'constructiva').

El primer paso consiste en utilizar factoriales (n!), que tienen la agradable propiedad de que cada uno contiene a TODOS los números anteriores a el en su factorización. Así, 3! = 3x2x1, y 6! = 6x5x4x3x2x1.

Para la prueba necesitamos que nos números sean consecutivos, así que pensemos en la siguiente serie, con n ≥ 1:

(n+1)! + 2, (n+1)!+3, (n+1)!+4 ... (n+1)+n+1

Es evidente que los números que genera esta serie son consecutivos (y positivos). ¿Cómo podemos saber si son compuestos ( = divisibles por algún número diferente de 1 y de sí mismos)?

Cojamos, por ejemplo, n=3. Entonces la serie se vuelve:

(4)! + 2, (4)!+3, (4!)+4

Sabemos que 4! = 4x3x2x1. Entonces 2 divide a 4! y (evidentemente), 2 se divide a sí mismo, así que 2 divide a (4)! + 2, que es un número compuesto. El siguiente, (4)!+3, es claramente el sucesor del anterior; 3 lo divide, e igualmente se divide a sí mismo. Igualmente, el siguiente, (4!)+4 es sucesor del anterior, y sus dos sumandos son divisibles por cuatro. Si los calculamos, hemos generado tres números consecutivos, 26, 27 y 28, que son todos compuestos (el siguiente, 29, es primo).

Es trivial constatar que la fórmula es ampliable infinitamente, y que funcionará con n más grandes por el mismo motivo (el factorial siempre incluirá entre sus factores a todos los números anteriores, y nos valdrá hasta (n+1)! + n + 1 para cualquier n > 1; y todos los sumandos acompañantes y menores que (n+1) serán divisibles por sí mismos). Si n = 3 nos generaba 3 compuestos consecutivos, n = 1 nos genera 1 (4), n = 2 nos genera 2 (8, 9), 4 nos genera 4 (120, 121, 122, 123, 124) y así sucesivamente.

Incidentalmente, a veces el siguiente(s) en la secuencia también son compuestos (en el último caso, 125 y 126 lo son), pero la fórmula sólo nos los garantiza para el n escogido.

Este demostración me tuvo día y medio atascado; sospecho que porque esperaba inconscientemente un mismo divisor para todos ellos.

Lenguaje matemático - ejercicios del tema 2 (3)

Aquí van.

Lema de Euclides y sus corolarios

Vuelvo a pelear con el libro de Matemática Discreta, y avanzando a paso de caracol. En una reciente videoconferencia introduciendo el curso, el profesor (y uno de los autores del volumen) Emilio Bujalance deja claro que hay que avanzar lenta y metódicamente con el libro (no es una lectura como la de una novela; hay que pararse, pensar, intentar realmente entender lo que se lee), pero temo que con este grado de dificultad, necesitaría todo el curso y por lo menos 2-3 horas diarias para poder completarlo. Ya veremos...

Hoy me proponía avanzar muy mucho en la sección 1.2 dedicada a los números primos, pero ya entre las primeras páginas, me topé con dificultades con un corolario del Lema de Euclides que me llevó un par de horas y algunas consultas poder comprender. Voy a intentar explicármelo con mis propias palabras como posible recordatorio para el futuro y para memorizarlo mejor.

La lema (¿el lema? ¿Cual es el género de esta palabra?), inserta en en contexto de temas de primalidad y co-primalidad, viene a formular lo siguiente:

-Dados 3 números enteros, a, b, c...

-Si a y c son coprimos entre sí...

-Y c divide al producto de bc...

ENTONCES, c necesariamente divide a b.

A priori, esto parece de sentido común (seguramente porque estoy aplicando el conocimiento informal de estudiante, frente a lo que se explicará rigurosamente más adelante en el libro, a la factorización de números en sus constituyentes primos). El libro lo demuestra de un modo bastante sencillo: si a y c son coprimos (=su mayor divisor común es 1), luego por la Identidad de Bezout, pueden representarse de la forma ax + cy = 1. Si multiplicamos ambos lados por b, tenemos bax + bcy = b. Es obvio que c divide a bcy; por el tercer punto que pusimos arriba, como c divide a ab, dividirá a bax; si divide a cada uno de los sumandos de la izquierda, tiene que poder dividir la igualdad de la derecha, y c divide a b.

(Incidentalmente, conviene dejar aclaradas las definiciones de primalidad y coprimalidad: un número primo es un entero mayor que 1 que sólo es divisible por sí mismo y por 1; números coprimos son aquellos que, sean o no primos, no comparten divisores comunes más allá del 1).

Los problemas me vinieron con un coralario de esta lema. El corolario establecía la siguiente identidad:

-Sea p un número entero mayor que 1...

-Si para TODAS las parejas de números enteros a, b cuyo producto, ab es divisible por p...

-P divide a uno (o a ambos) factores, esto es lo mismo que decir que...

ENTONCES p es un número primo (de hecho, esta puede ser una definición alternativa de número primo).

El problema que tuve fue básicamente que no percibía con claridad que esta relación entre p, a y b sólo era válida para TODAS las parejas. En efecto, es fácil topar números p mayores que 1 que dividen a un producto de números y a cada uno de los factores sin que p sea primo (por ejemplo, p = 4, a = 12, c = 16), pero si tenemos que tener en cuenta la totalidad de parejas a y b cuyo producto es divisible por p, entonces es fácil encontrar parejas donde este p no podría dividir a los factores: los casos en que los factores son menores que p. En nuestro ejemplo, p = 4, a = 2, b = 2. Si p es primo esto no pasará, porque tendremos al primo entre los factores (abierta o soterradamente) de a y/o de b).

El segundo corolario era más sencillo, y simplemente expandía esta regra de dos números, a y b, a una serie tan extensa como se quiera.

Lenguaje matemático - ejercicios del tema 2 (2)

Por fin he acabado los 24 ejercicios: son 13 páginas por las dos caras al final. En algunos he tenido que consultar la parte de las soluciones simplemente para entender qué es lo que se me pedía, pero en la mayoría no ha hecho falta. Algunos han sido relativamente fáciles, aunque en los casos más frecuentes, he tenido que estrujar el cerebro.

Los que más problemas me dan suelen ser los de 'demostrar'. Intentaré quizás mañana o pasado reconstruír uno de ellos, y ver si soy capaz.

¿Planes para los próximos días? Voy a volver mañana al libro de Discreta, intentando avanzar bien en la sección 1.2 (Números Primos). Por lo que toca a Lenguaje, voy a procurar ir haciendo los ejercicios de final de tema al mismo tiempo que la lectura de las partes de éste, para evitar eternizarme y tener todo más fresco.